Buried within the ancient ruins of Larsa, a 3,700-year-old clay tablet known as Plimpton 322 has fascinated mathematicians and historians for generations. Its true significance long remained a mystery, but recent breakthroughs have uncovered that this artifact contains an advanced form of trigonometry, predating Greek knowledge by over a thousand years. With its detailed cuneiform script and base-60 number system, this tablet provides a remarkable insight into the mathematical brilliance of the Babylonian civilization.
The Babylonian Clay Tablet: A 3,700-Year-Old Mathematical Marvel
In the realm of ancient artifacts, a 3,700-year-old Babylonian clay tablet known as ‘Plimpton 322’ has fascinated both mathematicians and historians. Found amidst the ruins of the ancient city of Larsa in modern-day Iraq, this tablet has intrigued scholars for decades due to its mysterious numerical inscriptions. However, its true significance remained a mystery until Dr. Daniel Mansfield, an Australian mathematician from the University of New South Wales, decoded its secrets. His groundbreaking work revealed that this artifact contains a sophisticated form of trigonometry, predating the Greek system by over a thousand years.
Unveiling the Origins and Age of Plimpton 322
Plimpton 322 was discovered in 1894 during excavations in Larsa, a city located along the Euphrates River. Unlike other artifacts found at the site, this clay tablet stood out due to its numerical markings. It dates back to approximately 1800 BCE, during the height of the Babylonian civilization. Despite its early discovery, the tablet remained largely unnoticed and stored in the Istanbul Archaeological Museum for years. However, recent research has brought this mathematical relic into the spotlight, shedding light on its profound historical and scientific importance. According to Dr. Mansfield, “It’s the only known example of a cadastral document from the Old Babylonian period, which is a plan used by surveyors to define land boundaries.”

Decoding the Babylonian Tablet: Dr. Mansfield’s Breakthrough
The recent study of Plimpton 322 was led by Dr. Mansfield and Associate Professor Norman Wildberger, with their findings published in Historia Mathematica, the journal of the International Commission on the History of Mathematics. Dr. Mansfield initially came across the tablet while preparing study material for his students, and his curiosity led to a deeper exploration of its numerical inscriptions.
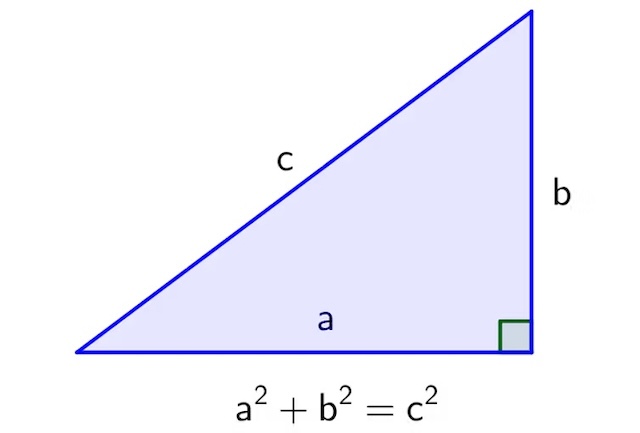
The clay tablet features four columns and 15 rows of numbers written in cuneiform script. At first glance, it seemed to be a mere list of numbers. However, Dr. Mansfield soon realized that these numbers corresponded to Pythagorean triples, a set of three whole numbers that satisfy the equation a² + b² = c². This relationship describes the sides of right-angled triangles, indicating that the Babylonians had knowledge of trigonometric principles. The rows on the tablet represent a sequence of 15 right-angle triangles, each with a progressively decreasing inclination.

What makes this discovery even more remarkable is that the Babylonians used a base-60 (sexagesimal) number system. This allowed for a high degree of precision in their calculations, far exceeding the accuracy of our modern base-10 (decimal) system. As Dr. Mansfield notes, “The base-60 system allowed for far more accurate calculations than our decimal-based system, which tends to round off numbers.” This method enabled them to calculate land boundaries and construct perfectly accurate right angles without complex tools.

The Advanced Accuracy of Babylonian Mathematics
The use of the base-60 number system was a key factor in the Babylonians’ mathematical accuracy. Unlike modern trigonometry, which often involves approximations and irrational numbers, the Babylonian method was based on exact ratios between the sides of triangles. For example, one of the Pythagorean triples found on Plimpton 322 is 119, 120, and 169—a far more complex set of numbers than the well-known 3, 4, and 5 triple. By focusing on whole number ratios, the Babylonians were able to create highly accurate right angles, useful for practical tasks like surveying land and construction.
Dr. Mansfield explained that the Babylonians’ approach to trigonometry was not concerned with angles as we understand them today. Instead, they developed an alternative “proto-trigonometry” based on ratios, specifically tailored to their needs in land measurement. This practical application of mathematics reveals a society that was highly advanced in its use of numerical systems long before the Greeks formalized the study of triangles.

A New Perspective on the History of Trigonometry
The discovery and decoding of Plimpton 322 challenge long-held beliefs about the origins of trigonometry. Historically, the Greek astronomer Hipparchus, who lived around 120 BCE, was regarded as the father of trigonometry. His “table of chords” was considered the earliest known trigonometric table. However, Dr. Mansfield’s research reveals that the Babylonians had developed a form of trigonometry more than a thousand years earlier.
Unlike the Greeks, whose trigonometry was centered around astronomy and the study of the heavens, the Babylonians developed their system for practical, earth-bound purposes. This proto-trigonometry was crucial for land measurement and defining boundaries, offering a glimpse into the societal needs that drove mathematical innovation in ancient Babylon.

Conclusion
The decoding of the 3,700-year-old Babylonian clay tablet by Dr. Daniel Mansfield has reshaped our understanding of early mathematics. The Babylonians’ method, based on the use of exact ratios and the base-60 system, reveals a form of trigonometry that was both practical and remarkably accurate. Their mathematical prowess, now revealed through Plimpton 322, underscores the advanced state of Babylonian society and offers new insights into the development of mathematical thought in the ancient world.
This discovery not only adds a new chapter to the history of mathematics but also highlights the importance of ancient artifacts in unraveling the knowledge of past civilizations. The Babylonian tablet is a testament to human ingenuity, demonstrating that the search for understanding the world through numbers is a pursuit as old as civilization itself.
